2024/02/01: 9h30
Speaker :
Guilherme Dias da Fonseca (LIS)
Title : Shadoks Approach to Convex Covering and Other CG:SHOP Challenges
Abstract: The CG:SHOP Challenge is a geometric optimization challenge organized annually as part of the prestigious SoCG conference. A different problem is proposed each year and the Shadoks team obtained several good results in the last 6 years. We describe these 6 problems, general algorithmic ideas, and strategy used in CG:SHOP 2023. The CG:SHOP 2023 challenge consisted of 206 instances, each being a polygon with holes. The goal was to cover each instance polygon by a small number of convex polygons inside the instance polygon (fewer polygons mean a better score). Our strategy was the following. We find a big collection of large (often maximal) convex polygons inside the instance polygon and then solve several set cover problems to find a small subset of the collection that covers the whole polygon.
( Paper:
https://arxiv.org/abs/2303.07696 )

10h10
Speaker :
Bruno Lévy (INRIA, U. Paris-Saclay)
Title : A Lagrangian method for fluids with free boundaries
Abstract: In this presentation, I’ll describe a numerical simulation method for free-surface fluids. I will start by giving an intuitive understanding of the physical phenomena involved in fluid dynamics, pressure, viscosity and surface tension. Then I will detail the numerical simulation method, based on the Gallouet-Mérigot numerical scheme, that describes the fluid as a set of cells, that can deform, but that keep a constant volume, and that follow the motion of the fluid (Lagrangian method). The constant volume constraint takes the form of a partial semi-discrete optimal transport. I will present the geometric and numerical aspects of this optimal transport problem.
The volume conservation constraint takes the form of a partial semi-discrete optimal transport problem. The solution of this transport problem determines the nature of the cells, that correspond to the intersection between Laguerre cells and balls.
( Pause Café : 11:10 – 11:30 )
11h30
Speaker :
Alexandra Bac (LIS)
Title : Combinatorial duality
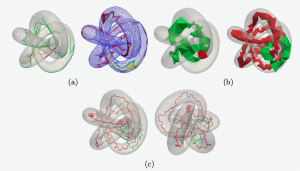
Abstract: Alexander duality establishes the relation between the homology of an object and the cohomology of its complement in a sphere. For instance, if X is a subset of the 2-dimensional sphere S2, then each hole of X corresponds to a connected component of S2 \ X, and by symmetry, each hole of S2 \ X corresponds to a connected component of X.
In this work we present a new combinatorial and constructive proof of Alexander duality that provides an explicit isomorphism. The proof shows how to compute this isomorphism using a combinatorial tool called homological colorings. It also provides a one-to-one map between the holes of the object and the holes of its complement, which we use for representing the holes of an object embedded in R3.
 10h10
Speaker : Bruno Lévy (INRIA, U. Paris-Saclay)
Title : A Lagrangian method for fluids with free boundaries
Abstract: In this presentation, I’ll describe a numerical simulation method for free-surface fluids. I will start by giving an intuitive understanding of the physical phenomena involved in fluid dynamics, pressure, viscosity and surface tension. Then I will detail the numerical simulation method, based on the Gallouet-Mérigot numerical scheme, that describes the fluid as a set of cells, that can deform, but that keep a constant volume, and that follow the motion of the fluid (Lagrangian method). The constant volume constraint takes the form of a partial semi-discrete optimal transport. I will present the geometric and numerical aspects of this optimal transport problem.
The volume conservation constraint takes the form of a partial semi-discrete optimal transport problem. The solution of this transport problem determines the nature of the cells, that correspond to the intersection between Laguerre cells and balls.
( Pause Café : 11:10 – 11:30 )
10h10
Speaker : Bruno Lévy (INRIA, U. Paris-Saclay)
Title : A Lagrangian method for fluids with free boundaries
Abstract: In this presentation, I’ll describe a numerical simulation method for free-surface fluids. I will start by giving an intuitive understanding of the physical phenomena involved in fluid dynamics, pressure, viscosity and surface tension. Then I will detail the numerical simulation method, based on the Gallouet-Mérigot numerical scheme, that describes the fluid as a set of cells, that can deform, but that keep a constant volume, and that follow the motion of the fluid (Lagrangian method). The constant volume constraint takes the form of a partial semi-discrete optimal transport. I will present the geometric and numerical aspects of this optimal transport problem.
The volume conservation constraint takes the form of a partial semi-discrete optimal transport problem. The solution of this transport problem determines the nature of the cells, that correspond to the intersection between Laguerre cells and balls.
( Pause Café : 11:10 – 11:30 )
 11h30
Speaker : Alexandra Bac (LIS)
Title : Combinatorial duality
Abstract: Alexander duality establishes the relation between the homology of an object and the cohomology of its complement in a sphere. For instance, if X is a subset of the 2-dimensional sphere S2, then each hole of X corresponds to a connected component of S2 \ X, and by symmetry, each hole of S2 \ X corresponds to a connected component of X.
In this work we present a new combinatorial and constructive proof of Alexander duality that provides an explicit isomorphism. The proof shows how to compute this isomorphism using a combinatorial tool called homological colorings. It also provides a one-to-one map between the holes of the object and the holes of its complement, which we use for representing the holes of an object embedded in R3.
11h30
Speaker : Alexandra Bac (LIS)
Title : Combinatorial duality
Abstract: Alexander duality establishes the relation between the homology of an object and the cohomology of its complement in a sphere. For instance, if X is a subset of the 2-dimensional sphere S2, then each hole of X corresponds to a connected component of S2 \ X, and by symmetry, each hole of S2 \ X corresponds to a connected component of X.
In this work we present a new combinatorial and constructive proof of Alexander duality that provides an explicit isomorphism. The proof shows how to compute this isomorphism using a combinatorial tool called homological colorings. It also provides a one-to-one map between the holes of the object and the holes of its complement, which we use for representing the holes of an object embedded in R3.